離散信号

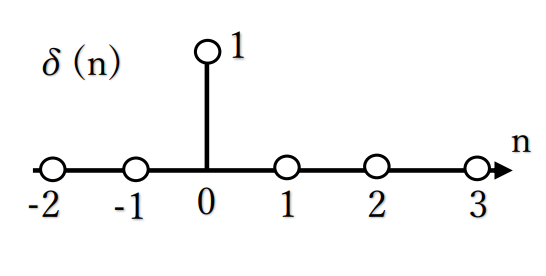
離散信号（りさんしんごう、（英: discrete signal）は時間が離散値をとる信号である。離散時間信号（りさんじかんしんごう、（英: discrete-time signal）とも。

概要

離散信号は時間が離散値をとる信号であり（⇒ #定義）、配列になぞらって $x[n]$ でしばしば表記される（⇒ #表記）。離散信号は周期的な場合があり、これは周期的な連続信号とは異なる特有の振る舞いをする（⇒ #周期性）。離散信号は連続信号の標本化でも得られる（⇒ #連続信号との関係）。

定義

離散信号は標本化された連続時間信号とも理解できる。系列の各値は標本値（sample、サンプル）と呼ばれる。

表記

離散時間信号であることを強調する場合、整数 $n$ を用いて次のように表記される。

$x(nT)$ : 連続時間信号 $x(t)$ と同じ時間軸で周期 $T$ ごとに値が定義（標本化）
$x[n]$ : 配列ライク（nはインデックス = 整数 = 離散的）
$x_{n}$ : 系列ライク（nはインデックス = 整数 = 離散的）

周期性

離散信号 $x[n]$ は周期関数の定義を満たしうる、つまり周期的たりうる。

周期

周期が定義可能な周期的離散信号では、周期 $S\in \mathbb {Z^{ }}$ $[sample]$ が見出だせる。

離散信号はその定義から隣り合うサンプル間に値が存在しない。そのため周期は正の整数値のみを取る。この値を用いて離散信号の周期性は $x[n]=x[n S]\quad \forall n\in \mathbb {N}$ として表現できる。

正規化角周波数

正規化角周波数は周期的な離散信号における1サンプルあたりの位相変化量である。

正規化角周波数 $\omega$ の単位は $[rad/sample]$ であり、定義域は $-\pi \leq \omega \leq \pi$ （あるいは $0\leq \omega \leq 2\pi$ ）である。

また標本化周期 $T_{s}$ および（非正規化）角周波数 $\Omega$ との間に

\Omega \ [rad/s]*T_{s}\ [s/sample]=\omega \ [rad/sample]

の関係が成立する。

連続信号との関係

連続信号は離散信号と対になる概念である。連続信号は時間が連続値をとる信号であり、離散信号の対義語にあたる。

連続信号から離散信号への変換

離散信号 $x[n]$ は連続信号 $x(t)$ の標本化でも得られる。すなわち標本化周期 $T_{s}$ を用いて $x[n]=x(nT)$ とすることで飛び飛びの値を取得し離散信号にできる。また離散信号の一種であるデジタル信号は、アナログ-デジタル変換（標本化量子化）により連続信号の一種であるアナログ信号から得られる。

周期的な連続信号と周期的な離散信号の違い

連続時間における周期信号が離散時間でも周期性をもつとは限らない。

例えば連続信号 $x(t)=cos(2/T_{s}*t)$ を標本化した離散信号 $x(nT_{s})=cos2n$ を考える。 $x(nT_{s})=1$ となる $n$ は整数かつ $n=\pi k\ (k\in \mathbb {Z} )$ を満たす必要があるが、これは $n=0$ しか存在しない。ゆえに $x(0)=x(0 S)$ を満たす $S$ が存在しない、つまり $x(t)=cos(2/T_{s}*t)$ は連続時間で周期性を持っていても標本化された離散時間では周期性を持たない。